
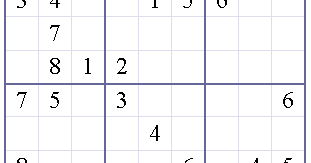

The graph coloring code is based on the Graph Coloring Kata with the following changes: However, trying to use more than 8 qubits (2 empty squares) in a simulation becomes very slow, so here we only run it for 1 or 2 missing squares in a 9x9 puzzle. The code can also solve 9x9 Sudoku puzzles using 4 qubits per number. This allows a 4x4 puzzle to be solved using 2 qubits per missing number. The numbers are changed to 0 to 3 and 0 to 8 and then converted back. However, when solving this using a quantum program and encoding these values into qubits, Note that the puzzles are initially defined in C# using numbers from 1 to 4, or 1 to9. Similarly, startingNumberConstraints is the array of (Cell#, constraint).įor example, the constraint that empty cell 0 can't have value 1 or 3 is encoded as startingNumberConstraints =. A list of constraints on empty squares to the initial numbers in the puzzle (starting numbers)įor example, for the row above the empty squares have indices: _Īnd emptySquareEdges is the array of edges.įor example, cell 0 can't have the same number (color) as cell 1, so emptySquareEdges =.A list of edges connecting empty squares.We define the puzzle using 2 data structures. To reduce the number of qubits, we only use qubits for empty squares.Įach empty square gets 2 qubits to encode the numbers 0 to 3. In the above example, the constraints for the top row are _ Graph edges are the constraints preventing squares from having the same values. In our case, graph nodes are puzzle squares and colors are the Sudoku numbers. Sudoku is a graph coloring problem where graph edges must connect nodes of different colors. The numbers 0 to 3 may only appear once per row, column and 2x2 sub squares. The code supports both 4x4 and 9x9 Sudoku puzzles. This program demonstrates solving Sudoku puzzle using Grover's algorithm.


 0 kommentar(er)
0 kommentar(er)
